Циліндр – це симетрична просторова фігура, властивості якої розглядають в старших класах школи в курсі стереометрії. Для його опису використовують такі лінійні характеристики, як висота і радіус підстави. У цій статті розглянемо питання стосовно того, що таке осьовий переріз циліндра, і як розрахувати його параметри через основні лінійні характеристики фігури.
Геометрична фігура
Спочатку дамо визначення фігури, про яку піде мова в статті. Циліндр являє собою поверхню, утворену паралельним переміщенням відрізка фіксованої довжини вздовж деякої кривої. Головною умовою цього переміщення є те, що відрізок площині кривої належати не має.
На малюнку нижче показаний циліндр, крива (напрямна) якого є еліпсом.
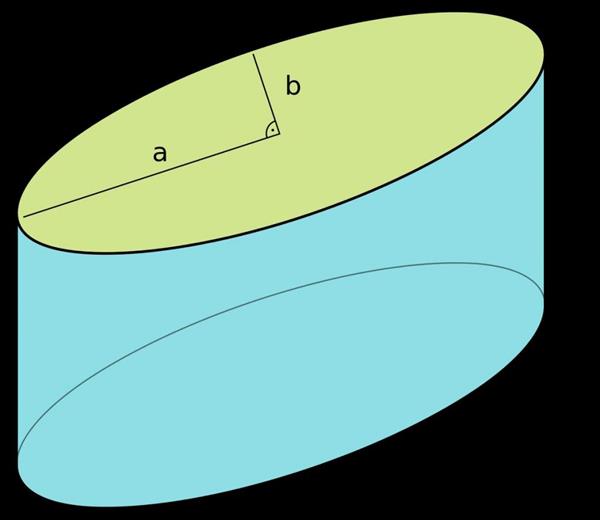
Тут відрізок довжиною h є його утворює і висотою.
Видно, що циліндр складається з двох однакових підстав (еліпси в даному випадку), які лежать у паралельних площинах, і бічної поверхні. Останньої належать всі точки утворюють ліній.
Прямий і похилий циліндри
Перед тим як переходити до розгляду осьового перерізу циліндра, розповімо, які типи цих фігур бувають.
Якщо твірна лінія перпендикулярна підстав фігури, тоді говорять про прямому циліндрі. В іншому випадку циліндр буде похилою. Якщо з’єднати центральні точки двох підстав, то отримана пряма називається віссю фігури. Наведений рисунок демонструє різницю між прямим і похилим циліндрами.
Видно, що для прямої фігури довжина утворює відрізка збігається зі значенням висоти h. Для похилого циліндра висота, тобто відстань між підставами, завжди менше довжини твірної лінії.
Далі охарактеризуємо осьові перерізи обох типів циліндрів. При цьому будемо розглядати фігури, підставами яких є коло.
Осьовий переріз прямого циліндра
Осьовим називається будь-який перетин циліндра, яка містить його вісь. Це визначення означає, що осьовий переріз буде завжди паралельно твірної лінії.
У прямому циліндрі вісь проходить через центр кола і перпендикулярна до його площини. Це означає, що розглянуте переріз коло буде перетинати за його діаметру. На малюнку показана половинка циліндра, яка вийшла в результаті перетину фігури площиною, що проходить через вісь.
Не складно зрозуміти, що осьовий переріз прямого круглого циліндра являє собою прямокутник. Його сторонами є діаметр d підстави і висота h фігури.
Запишемо формули для площі осьового перерізу циліндра і довжини hd його діагоналі:
S = h*d;
hd = √(h2 + d2)
Прямокутник має дві діагоналі, але обидві вони дорівнюють один одному. Якщо відомий радіус підстави, то не складно переписати ці формули через нього, враховуючи, що він в два рази менше діаметра.
Осьовий переріз похилого циліндра
Малюнок вище демонструє похилий циліндр, виготовлений з паперу. Якщо виконати його осьовий переріз, то вийде вже не прямокутник, а паралелограм. Його сторони – це відомі величини. Одна з них, як і у випадку перетину прямого циліндра, що дорівнює діаметру d підстави, інша ж – довжина утворює відрізка. Позначимо її b.
Для однозначного визначення параметрів паралелограма недостатньо знати його довжини сторін. Необхідний ще кут між ними. Припустимо, що гострий кут між направляючою та підставою дорівнює α. Він же і буде кутом між сторонами паралелограма. Тоді формулу для площі осьового перерізу похилого циліндра можна записати наступним чином:
S = d*b*sin(α)
Діагоналі осьового перерізу циліндра похилого розрахувати дещо складніше. Паралелограм має дві діагоналі різної довжини. Наведемо без виведення вирази, які дозволяють розраховувати діагоналі паралелограма по відомим сторонам і гострого кута між ними:
l1 = √(d2 + b2 – 2*b*d*cos(α));
l2 = √(d2 + b2 + 2*b*d*cos(α))
Тут l1 і l2 – довжини малої і великої діагоналей відповідно. Ці формули можна отримати самостійно, якщо розглянути кожну діагональ як вектор, ввівши прямокутну систему координат на площині.
Завдання з прямим циліндром
Покажемо, як використовувати отримані знання для вирішення наступного завдання. Нехай дано круглий прямий циліндр. Відомо, що осьовий переріз циліндра – квадрат. Чому дорівнює площа цього перерізу, якщо площа поверхні всієї фігури становить 100 см2?
Для обчислення шуканої площі необхідно знайти або радіус або діаметр основи циліндра. Для цього скористаємося формулою для загальної площі Sf фігури:
Sf = 2*pi*r*(r + h)
Оскільки осьовий переріз являє собою квадрат, то це означає, що радіус r заснування в два рази менше висоти h. Враховуючи це, можна переписати рівність вище у вигляді:
Sf = 2*pi*r*(r + 2*r) = 6*pi*r2
Тепер можна виразити радіус r, маємо:
r = √(Sf / (6*pi))
Оскільки сторона квадратного перерізу дорівнює діаметру основи фігури, то для обчислення його площі S буде справедлива наступна формула:
S = (2*r)2 = 4*r2 = 2*Sf / (3*pi)
Ми бачимо, що шукана площа однозначно визначається площею поверхні циліндра. Підставляючи дані в рівність, приходимо до відповіді: S = 21,23 см2.
