Трикутні, чотирикутні і шестикутні призми – це найпоширеніші об’ємні фігури серед інших подібних, які зустрічаються в побуті і природі. Вивченням їх властивостей займається стереометрія, або просторова геометрія. У даній статті розкриємо питання про те, як можна знайти площу бічної поверхні правильної трикутної призми, а також чотирикутної і шестикутної.
Що собою являє призма?
Перед тим як розраховувати площу бічної поверхні правильної трикутної призми та інших видів цієї фігури, слід розібратися, що вони собою представляють. Потім навчимося визначати, що цікавлять величини.
Призмою, з точки зору геометрії, називається об’ємне тіло, яке обмежене двома довільними однаковими многокутниками і n параллелограммами, де n – це число сторін одного многокутника. Намалювати таку фігуру легко, для цього слід зобразити який-небудь багатокутник. Потім провести з кожної його вершини відрізок, який дорівнює по довжині і паралельний всім іншим. Потім потрібно з’єднати кінці цих ліній між собою так, щоб вийшов ще один багатокутник, рівний вихідному.
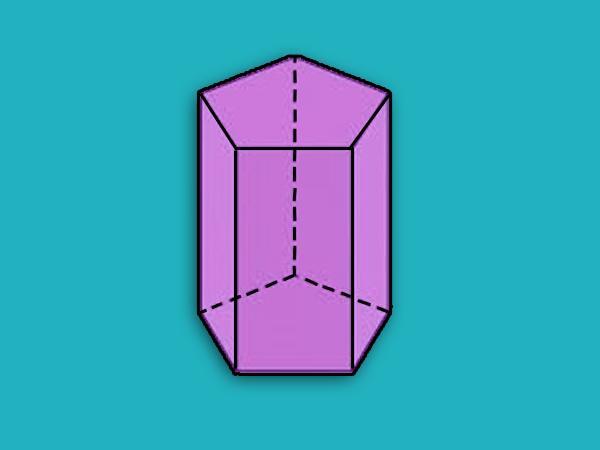
Вище видно, що фігура обмежена двома пятиугольниками (вони називаються нижнім і верхнім підставами фігури) і п’ятьма параллелограммами, які на рисунку відповідають прямокутникам.
Всі призми відрізняються один від одного двома головними параметрами:
- типом багатокутника, що лежить в основі фігури;
- кутами між параллелограммами і підставами.
Кількість сторін прямокутника дає назву призмі. Звідси отримуємо вище згадані трикутну, шестикутну та чотирикутну фігури.
Також вони різняться за величиною нахилу. Що стосується зазначених кутів, якщо вони рівні 90o, тоді таку призму називають прямою, або прямокутної (кут нахилу дорівнює нулю). Якщо деякі з кутів не є прямими, то фігура зветься косокутної. Відмінність між ними видно з першого погляду. Малюнок нижче демонструє ці різновиди.
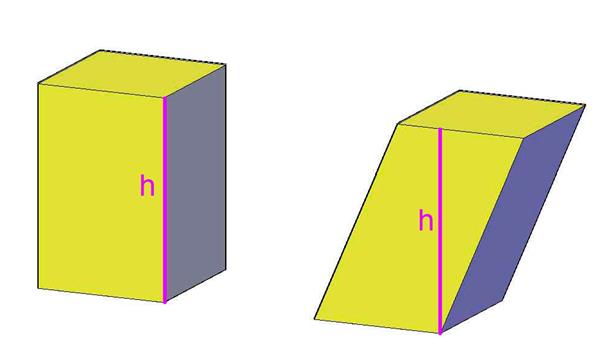
Як видно, висота h прямої призми збігається з довжиною її бічного ребра. У разі косокутної цей параметр завжди менше.

