Розділ фізики, який вивчає рух тіл по різних траєкторіях, називається кінематикою. Практично корисними типами переміщення об’єктів є рух по прямій і по колу. Розглянемо у статті, що являють собою ці типи руху, якими вони описуються формулами, а також наведемо зв’язок кутової та лінійної швидкості.
Рух по прямій
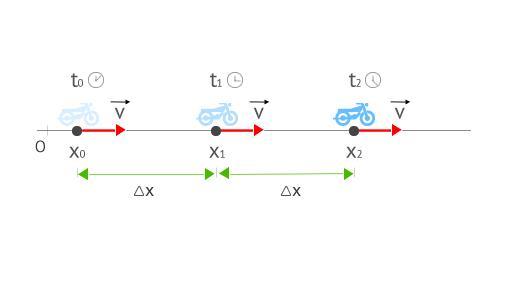
Зв’язок кутової та лінійної швидкості можна визначити, якщо знати, про яких величинах йде мова. Почнемо з лінійної швидкості.
Зі шкільної лави кожен знає, що переміщення об’єктів у просторі характеризується трьома основними величинами:
- пройдений шлях S;
- час руху t;
- швидкість v.
Формула, що зв’язує в єдине рівність названі величини, наведена нижче:
S = v * t.
Наведене вираз описує рівномірний рух тіла по прямій лінії. У міжнародній системі одиниць СІ величина S вимірюється в метрах (м), t – в секундах (с), v – в метрах за секунду (м/с). Крім названих одиниць, шлях і час можуть виражати в кілометрах (км) і годинах (год), відповідно. Тоді швидкість буде виражатися в кілометрах в годину (км/год).
Записана формула може застосовуватися для вирішення широкого кола практичних завдань, наприклад, рух транспортних засобів по дорогах, рух кораблів і човнів по річках, політ птахів і так далі.
Рух по колу
Перед тим як перейти до висновку формули зв’язку лінійної та кутової швидкості, слід розглянути останню з точки зору фізики.
Кутова швидкість з’являється у фізиці, коли мова йде про обертових об’єктах. Прикладами можуть бути обертання колеса велосипеда, маховика автомобіля або планети навколо своєї зірки. Кутова швидкість тіла показує, на який кут в радіанах воно повертається за одиницю часу. Зазвичай цю величину позначають грецькою буквою ω (омега). Вона вимірюється в радіанах в секунду (рад/с).
За аналогією з лінійним випадком можна назвати три головних величини, які описують рух по колу з постійною кутовий швидкістю:
- кут повороту θ;
- час t;
- кутова швидкість ω.
Відповідна формула, яка пов’язує ці величини, виглядає так:
θ = ω * t.
Кут повороту тіла θ навколо осі обертання вимірюється в радіанах. Нагадаємо, що окружність має 2 * pi радіан (близько 6,28). Якщо отримане за формулою значення θ виявилося більше, ніж 2 * pi, то це означає, що тіло зробило більше одного оберту навколо осі.
Таким чином, записане вираз дозволяє розрахувати число оборотів, чинених тілом за відомий проміжок часу t.
Зв’язок кутової та лінійної швидкості
Тепер можна розглянути це питання. Припустимо, що тіло, що має лінійну швидкість v, обертається по колу радіусом R. Щоб отримати між лінійною і кутовою швидкістю зв’язок, розглянемо, який час знадобиться тілу, щоб зробити один повний оборот. Оскільки пройдений шлях дорівнює довжині кола, то наступне вираз буде справедливим:
t = S/v = 2 * pi * R/v.
Тепер скористаємося кутовими величинами. За знайдене час одного обороту t, тіло повернеться точно на 2 * pi радіан. Останнє означає, що його кутова швидкість буде дорівнює:
ω = θ/t = 2 * pi/t.
Підставимо розраховане вище час t і отримаємо між кутовою та лінійною швидкістю зв’язок:
ω = 2 * pi/t = 2 * pi/(2 * pi * R/v) = v/R.
Отриману формулу можна записати у двох видах:
ω = v/R;
v = ω * R.
Кожне з виразів застосовується в залежності від того, яка величина в умові задачі відома. Формули дозволяють зробити важливий висновок: чим більший радіус орбіти обертання, тим більше буде лінійна швидкість при постійній кутовій швидкості.
Далі вирішимо цікаву завдання на застосування отриманих формул.
Що швидше – Земля або Марс?
Відомо, що Земля і Марс є 3-й і 4-й планетами Сонячної системи, відповідно. Обидві планети рухаються приблизно за круглим орбітах. Відстань від нашої зірки до Землі одно 149 597 870,691 км, а один оборот навколо неї вона робить за 365,256 днів. Марс розташована від Сонця на відстані 227 936 640 км, і один оборот навколо нього робить за 686,971 земних дня. Необхідно визначити і порівняти лінійні швидкості планет.
Кутова швидкість планети може бути розрахована за формулою:
ω = 2 * pi/T.
Де T – період (час вчинення одного обороту навколо зірки). Підставляючи ω в формулу для v, отримуємо:
v = 2 * pi * R/T.
Переведемо час обороту планет годинник і підставимо дані в цю рівність, одержимо:
- для Землі: v = 2 * 3,14 * 149597870,691/(365,256 * 24) ≈ 107,2 тис. км/год;
- для Марса: v = 2 * 3,14 * 227936640/(686,971 * 24) ≈ 86,8 тис. км/ч.
Обидві цифри є величезними. Так, Земля за одну годину пролітає в космосі відстань, практично рівну трьом її колах по екватору. Отримані швидкості свідчать, що Земля рухається швидше Марса, і її швидкість на 24 % більше марсіанської.
