Одним з симетричних поліедрів, властивості якого вивчає стереометрія, є піраміда. В даній статті розглянемо детальніше такі питання: що таке усічена піраміда, як її можна отримати і якими властивостями вона характеризується.
Повна піраміда
Перш ніж розкривати питання, що таке усічена піраміда, слід дати визначення піраміди в загальному випадку.
Під пірамідою в геометрії розуміють фігуру в тривимірному просторі, яка складається з n трикутних граней і однієї n-вугільної сторони, яка називається основою. Уявити собі піраміду досить просто: необхідно подумки з’єднати всі кути n-кутника з деякою однією точкою в просторі. Малюнок нижче показує фігуру, яка при цьому виходить.
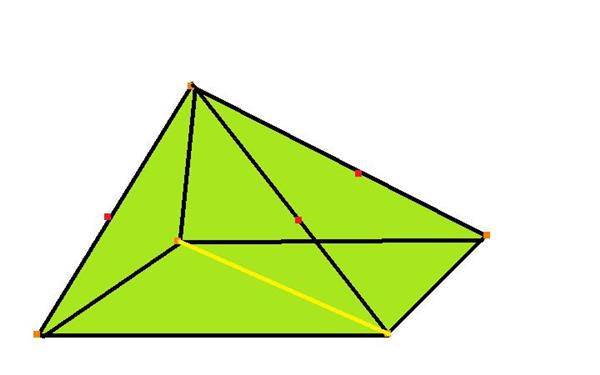
Тут ми бачимо, що кути чотирикутного підстави з’єднані відрізками з однією точкою, яка називається вершиною піраміди. Бічна поверхня фігури утворена чотирма різними трикутниками.
Якщо всі трикутники бічній поверхні будуть однаковими і равнобедренными, то така фігура називається прямий пірамідою. Якщо до того ж підстава буде представляти правильний n-кутник, наприклад, квадрат, то говорять про піраміду правильної.
Усічена піраміда
Розглянута вище фігура називається повною пірамідою. Тепер покажемо, що таке усічена піраміда і як її можна отримати з повною.
Нехай у нас є повна фігура з п’ятикутним підставою. Вона показана нижче на малюнку зліва.
Візьмемо довільну площину і відсічемо верхню частину у повній піраміди. Площина розділить початкову фігуру на дві частини: верхня представлятиме також піраміду, а нижня – це вже усічена піраміда (див. праве зображення на малюнку).
Зауважимо, що в даному випадку ми вибрали січну площину, яка паралельна основі вихідної фігури. Отримана з правильної фігури з допомогою паралельного перерізу усічена піраміда також буде називатися правильною.
Рисунок також показує, що підстави усіченої піраміди (пятиугольники в прикладі) утворені подібними правильними многокутниками, при цьому розмір верхнього буде завжди менше, ніж нижнього. Бічна поверхня цієї фігури, на відміну від повної піраміди, утворена равнобедренными трапеціями.
Якщо в основі усіченої піраміди лежить n-кутник, тоді вона має 2 × n вершин, 3 × n ребер і n + 2 сторони.
Двома важливими геометричними параметрами даної фігури є площа її поверхні та об’єм.
Поверхня усіченої піраміди
Розглянувши, що таке усічена піраміда, перейдемо до вивчення її поверхні. Під останньою розуміють сукупність усіх граней, що утворюють фігуру. Найпростіше властивості поверхні вивчати на прикладі розгортки. Малюнок нижче показує розгортку для піраміди з п’ятикутними підставами.
Щоб обчислити площу всій її поверхні, необхідно скласти площа двох підстав і площа всіх трапецій. Відповідна формула має вигляд:
S = So1 + So2 + 1/2 × (Po1 + Po2) × Ap.
У цьому вираженні перші два члена, тобто So1 і So2, являють собою площі підстав. Третій член – це сумарна площа всіх трапецій, яка дорівнює половині добутку суми периметрів підстав Po1 і Po2 на апофему (висоту) трапеції Ap.
Наприклад, для випадку з правильної чотирикутної усіченої піраміди ця формула перепишеться у вигляді:
S4 = B2 + b2 + 2 × (B + b ) × Ap.
Де B, b – довжини сторін великого і малого квадратних підстав відповідно.
Об’єм зрізаної піраміди
Для визначення обсягу розглянутої фігури необхідно знати її висоту h, а також площі обох підстав So1 і So2. Якщо зазначені характеристики відомі, тоді для визначення об’єму усіченої піраміди слід скористатися формулою:
V = 1/3 × h × (So1 + So2 + √ (So1 × So2)).
Наприклад, для правильної чотирикутної фігури, довжини сторін підстав якої дорівнюють B і b, приходимо до наступного виразу для об’єму:
V = 1/3 × h × (B2 + b2 + B × b).
Приклад розв’язання задачі
Розглянувши, що таке усічена піраміда, а також розібравшись з необхідними для опису її характеристик формулами, покажемо, як їх використовувати на практиці.
Припустимо, що є шестикутна усічена фігура, яка показана нижче.
Необхідно розрахувати її обсяг, якщо відомі сторони підстав B і b і апофема Ap.
Для початку розрахуємо площу кожного з підстав, яка відповідає площі правильного шестикутника. Маємо:
So1 = 3 × √3/2 × B2;
So2 = 3 × √3/2 × b2.
Для визначення обсягу необхідно обчислити через Ap висоту h фігури. Розглядаючи зображений на малюнку прямокутний трикутник і застосовуючи теорему Піфагора, отримуємо:
h = √ (Ap2 – 3/4 × (B-b)2).
Тоді обсяг цієї шестикутної усіченої піраміди дорівнює:
V = √3/2 × √(Ap2 – 3/4 × (B-b)2) × (B2 + b2 + B × b).
Піраміди майя
Якщо єгипетські піраміди з точки зору геометрії являють собою правильні повні чотирикутні фігури, то аналогічні споруди індіанців майя є чотирикутними усіченими пірамідами.
Ці пам’ятки культури, що збереглися до наших днів, колись виконували подвійну роль для своїх жителів: з одного боку, вони служили гробницею вождям, з іншого ж боку, на їх верхньому підставі розташовувався храм, де жерці поклонялися богам.
