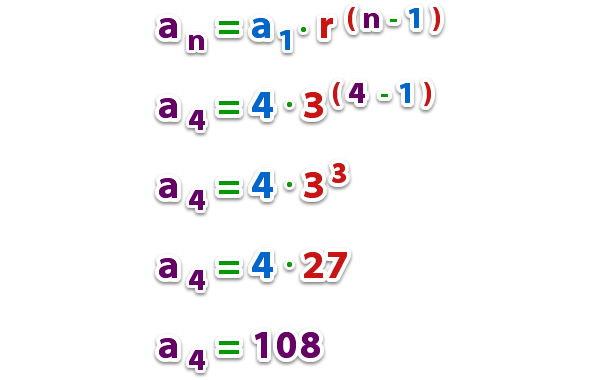Деякі завдання фізики і математики можуть бути вирішені з використанням властивостей числових рядів. Дві найпростіших числових послідовності, які вивчаються в школах, це алгебраїчна і геометрична. В даній статті розглянемо детальніше питання, як знайти суму нескінченної геометричної прогресії спадною.
Геометрична прогресія
Під цими словами розуміють такий ряд дійсних чисел, елементи ai якого задовольняють виразом:
ai = ai-1*r
Тут i – номер елемента в рядку, r – постійне число, яке називається знаменником.
Це визначення показує, що, знаючи будь-який член прогресії і його знаменник, можна відновити весь ряд чисел. Наприклад, якщо відомий 10-й елемент, то поділивши його на r, отримаємо 9-й елемент, потім, розділивши ще раз, отримаємо 8-й і так далі. Ці прості міркування дозволяють записати вираз, яке справедливо для розглянутого ряду чисел:
ai = a1*ri-1
Прикладом прогресії зі знаменником 2 може бути такий ряд:
1, 2, 4, 8, 16, 32, …
Якщо ж знаменник дорівнює -2, тоді виходить зовсім інший ряд:
1, -2, 4, -8, 16, -32, …
Геометрична прогресія є набагато більш швидкою, ніж алгебраїчна, тобто її члени швидко ростуть і швидко зменшуються.
Сума i членів прогресії
Для рішення практичних задач часто доводиться обчислювати суму декількох елементів розглянутої числової послідовності. Для цього випадку справедлива наступна формула:
Si = a1*(ri-1)/(r-1)
Видно, що для обчислення суми i членів необхідно знати всього два числа: a1 і r, що є логічним, оскільки вони однозначно визначають всю послідовність.
Щербатий послідовність і сума її членів
Тепер розглянемо окремий випадок. Вважатимемо, що модуль знаменника r не перевищує одиниці, тобто -1
Убуваючу геометричну прогресію цікаво розглянути, тому що нескінченна сума її членів прагне до кінцевого дійсному числу.
Отримаємо формулу суми нескінченної спадної геометричної прогресії. Це легко зробити, якщо виписати вираз для Si, наведеного в попередньому пункті. Маємо:
Si = a1*(ri-1)/(r-1)
Розглянемо випадок, коли i->∞. Оскільки модуль знаменника менше 1, то зведення його в нескінченну ступінь дасть нуль. Це можна перевірити на прикладі r=0,5:
0,52 = 0,25; 0,53 = 0,125; …., 0,520 = 0,0000009.
У результаті сума членів нескінченної геометричної прогресії спадної прийме форму:
S∞ = a1/(1-r)
Ця формула часто використовується на практиці, наприклад, для обчислення площ фігур. Її також застосовують при вирішенні парадокси Зенона Элейского з черепахою і Ахіллесом.
Очевидно, що розгляд суми нескінченної геометричної прогресії зростаючою (r>1), призведе до результату S∞ = +∞.
Завдання на знаходження першого члена прогресії
Покажемо, як слід застосовувати наведені вище формули на прикладі розв’язання задачі. Відомо, що сума нескінченної геометричної прогресії дорівнює 11. При цьому 7-й її член в 6 разів менше третього члена. Чому дорівнює перший елемент для цього числового ряду?
Для початку випишемо два вирази для визначення 7-го і 3-го елементів. Отримуємо:
a7 = a1*r6
a3 = a1*r2
Розділивши перше вираз на друге, і висловлюючи знаменник, маємо:
a7/a3 = r4 => r = 4√(a7/a3)
Оскільки відношення сьомого і третього членів дано в умові задачі, можна його підставити і знайти r:
r = 4√(a7/a3) = 4√(1/6) ≈ 0,63894
Ми розрахували r з точністю до п’яти значущих цифр після коми. Оскільки отримане значення менше одиниці, значить, прогресія є спадною, що виправдовує використання формули для її нескінченної суми. Запишемо вираз для першого члена через суму S∞:
a1 = S∞*(1-r)
Підставляємо в формулу відомі значення і отримуємо відповідь:
a1 = 11*(1-0,63894) = 3,97166.
Знаменитий парадокс Зенона з швидким Ахіллесом і повільної черепахою
Зенон Элейский – відомий грецький філософ, який жив у V столітті до н. е. До нашого часу дійшли деякі його апогей або парадоксів, у яких формулюється проблема нескінченно великого і нескінченно малого математики.
Одним із відомих парадоксів Зенона є змагання Ахіллеса і черепаху. Зенон вважав, що якщо Ахіллес надасть деяку перевагу черепасі у відстані, то він ніколи не зможе її наздогнати. Наприклад, нехай Ахіллес біжить в 10 разів швидше, ніж повзе тварина, яка для прикладу знаходиться на відстані 100 метрів попереду нього. Коли воїн пробіжить 100 метрів, то черепаха відповзе на 10. Пробігши знову 10 метрів, Ахіллес побачить, що черепаха відповзла ще на 1 метр. Міркувати так можна до нескінченності, відстань буде між спортсменами дійсно зменшуватися, але черепаха буде завжди знаходитися попереду.
Цей парадокс привів Зенона до висновку, що руху не існує, і всі навколишні переміщення об’єктів – це ілюзія. Звичайно ж, давньогрецький філософ помилявся.
Рішення парадоксу криється в тому, що нескінченна сума постійно зменшуються відрізків, прагне до кінцевого числа. У наведеному вище випадку для відстані, яке пробіг Ахіллес, отримаємо:
100 + 10 + 1 + 0,1 + 0,01 + …
Застосовуючи формулу суми нескінченної геометричної прогресії, одержимо:
S∞ = 100 /(1-0,1) ≈ 111,111 метрів
Цей результат показує, що дожене Ахіллес черепаху, коли вона проповзе всього 11,111 метрів.
Стародавні греки не вміли працювати з нескінченними величинами в математиці. Проте цей парадокс можна вирішити, якщо звернути увагу не на нескінченне число проміжків, які повинен подолати Ахіллес, а на кінцеве число кроків бігуна, необхідних для досягнення мети.
