Стереометрія – це розділ геометрії, що вивчає фігури, які не лежать в одній площині. Одним з об’єктів вивчення стереометрії є призми. У статті дамо визначення призмі з геометричної точки зору, а також коротко перерахуємо властивості, які для неї характерні.
Геометрична фігура
Визначення призми в геометрії звучить наступним чином: це просторова фігура, що складається з двох однакових n-кутників, що розташовані в паралельних площинах, з’єднаних один з одним своїми вершинами.
Отримати призму не представляє ніякої праці. Уявимо, що є два однакових n-кутника, де n – це число сторін або вершин. Помістимо їх так, щоб вони були паралельні один одному. Після цього вершини одного многокутника слід з’єднати з відповідними вершинами іншого. Утворена фігура буде складатися з двох n-вугільних сторін, які називаються підставами, і n чотирикутних сторін, що представляють собою в загальному випадку паралелограми. Сукупність паралелограмів утворює бічну поверхню фігури.
Існує ще один спосіб геометричного отримання даної фігури. Так, якщо взяти n-кутник і зробити його перенесення в іншу площину за допомогою паралельних відрізків рівної довжини, то в новій площині ми отримаємо вихідний багатокутник. Обидва багатокутника і всі паралельні відрізки, проведені з їх вершин, що утворюють призму.
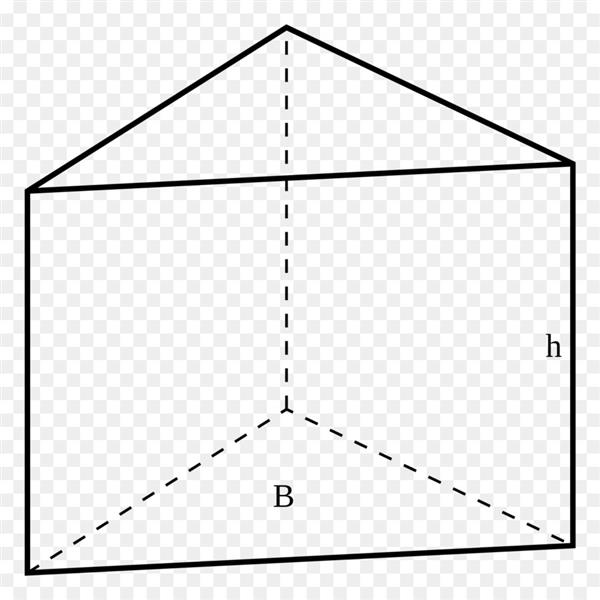
Малюнок вище демонструє трикутну призму. Так вона називається тому, що її заснування являють собою трикутники.

