Просторова геометрія займається вивченням властивостей об’ємних фігур та їх різного взаємного розташування. Дана стаття присвячена дослідженню характеристик такого полиэдра, як піраміда. Вписані та описані фігури в конус, куб будуть розглянуті.
Просторова фігура піраміда
Піраміда – геометрична фігура, обмежена n+1 межею, з яких одна грань є гратки з n сторонами, і n граней являють собою трикутники, сполучені між собою в одній вершині.
На малюнку нижче показані дві піраміди.
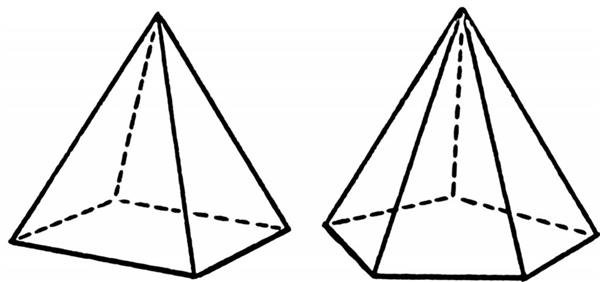
Ліва фігура складається з 5 граней, де гратки є чотирикутник, права – з шести граней, оскільки її багатокутник має п’ять сторін. Чотирикутник для лівої фігури і п’ятикутник для правої є підставами. Точка, де з’єднуються трикутники – це вершина піраміди.
Як геометрична фігура піраміда довільного типу може бути отримана так: необхідно взяти n-кутник і з’єднати всі його кути з деякою фіксованою точкою в просторі, яка, однак, не повинна лежати в площині n-кутника.
Кожна піраміда складається з n+1 сторони (межі), має 2*n ребер і n+1 вершину.

