З поділом математики на алгебру і геометрію навчальний матеріал стає складнішим. З’являються нові фігури та їх приватні випадки. Для того щоб добре розібратися в матеріалі, необхідно вивчити поняття, властивості об’єктів і супутні теореми.
Загальні поняття
Під чотирикутником мається на увазі геометрична фігура. Складається вона з 4-х точок. Причому 3 з них не розташовуються на одній прямій. Є відрізки, послідовно з’єднують зазначені точки.
Всі чотирикутники, що вивчаються в шкільному курсі геометрії, показані в наступній схемі. Висновок: будь-який об’єкт з представленого малюнка володіє властивостями попередньої фігури.
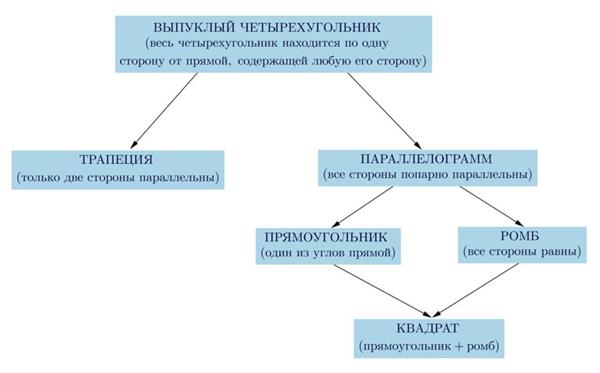
Чотирикутник може бути наступних видів:
- Паралелограм. Паралельність його протилежних сторін підтверджується відповідними теоремами.
- Трапеція. Чотирикутник, у якого підстави паралельні. Інші дві сторони – немає.
- Прямокутник. Фігура, у якої всі 4 кута = 90º.
- Ромб. Фігура, у якої всі сторони рівні.
- Квадрат. Поєднує в собі властивості останніх двох фігур. У нього всі сторони рівні і всі кути прямі.
Основне визначення даної теми – вписаний чотирикутник у коло. Воно полягає в наступному. Це фігура, навколо якої описана окружність. Вона повинна проходити через всі вершини. Внутрішні кути чотирикутника, вписаного в коло, в сумі дають 360º.
Не кожен чотирикутник може бути вписаний. Пов’язано це з тим, що серединні перпендикуляри 4-х сторін не можуть перетнутися в одній точці. Це зробить неможливим знаходження центру окружності, описаної близько 4-кутника.
Приватні випадки
З кожного правила є винятки. Так, у даній темі також є окремі випадки:
- Паралелограм, як такої, не може бути вписаний в окружність. Тільки його окремий випадок. Це прямокутник.
- Якщо всі вершини ромба знаходяться на описує лінії, то він є квадратом.
- Всі вершини трапеції знаходяться на межі кола. У такому разі говорять про равнобедренной фігурі.
Властивості вписаного у коло чотирикутника
Перед вирішенням простих і складних задач з заданої теми необхідно впевнитися у своїх знаннях. Без вивчення навчального матеріалу неможливо вирішити ні один приклад.
Теорема 1
Сума протилежних кутів чотирикутника, вписаного в коло, дорівнює 180º.
Доказ
Дано: чотирикутника АВСД вписаний в окружність. Її центр – точка О. Потрібно довести, що
Потрібно розглянути представлені фігури.
Аналогічним способом відбувається доказ для
Теорема 2
(Її часто називають зворотним) Якщо в чотирикутнику
Доказ
Дана сума протилежних кутів чотирикутника ABCD дорівнює 180º.
З курсу геометрії відомо, що через 3 точки чотирикутника можна провести окружність. Наприклад, можна задіяти точки A, B, C. Де буде знаходитися т. D? Є 3 припущення:
- Вона виявляється всередині кола. При цьому D не стосується лінії.
- Поза кола. Вона заступає далеко за межі окресленої лінії.
- Виявляється на окружності.
Слід припустити, що D розташовується всередині кола. Місце зазначеної вершини займає D. Виходить чотирикутник ABCD.
В результаті слід:
Якщо продовжити AD до перетину з наявною колом з центром у точці Е і з’єднати E і C, вийде вписаний чотирикутник ABCE. З першої теореми випливає рівність:
Згідно законам геометрії, вираз не має сили, оскільки
Подібним чином можна довести неправильність третього припущення, коли D виходить за кордон описаної фігури.
З двох гіпотез випливає єдино вірна. Вершина D розташовується на лінії окружності. Іншими словами, D збігається з E. Звідси випливає, що всі точки чотирикутника розташовуються на цій лінії.
З цих двох теореми випливають наслідки:
- Будь прямокутник може бути вписаний в окружність. Існує і інше слідство. Навколо будь-якого прямокутника може бути описана окружність.
- Трапеція з рівними стегнами може бути вписана в коло. Іншими словами це звучить так: навколо трапеції з рівними ребрами може бути описана окружність.
Кілька прикладів
Завдання 1. У коло вписано чотирикутник ABCD.
Рішення. Спочатку може здатися, що знайти відповідь буде важко.
1. Потрібно згадати властивості з цієї теми. А саме: сума протилежних кутів = 180º.
В геометрії краще дотримуватися принципу: знайти все, що можна. Потім пригодиться.
2. Наступний крок: використовувати теорему про суму кутів трикутника.
Відповідь:
Завдання 2. Дан BCDE – вписаний чотирикутник у коло.
Рішення.
- Необхідно знайти
Відповідь: < E = 96º.
Завдання 3. Дан вписаний чотирикутник у коло. Дані вказані на малюнку. Необхідно знайти невідомі величини x, y, z.
Рішення:
z = 180º – 93º = 87º (за Теоремою 1)
x = ½ * (58º + 106º) = 82º
y = 180º – 82º = 98º (за Теоремою 1)
Відповідь: z = 87º, x = 82º, y = 98º.
Завдання 4. Є вписаний чотирикутник у коло. Величини вказані на малюнку. Знайти x , y.
Рішення:
x = 180º – 80 = 100º
y = 180º – 71º = 109º
Відповідь: x = 100º, y = 109º.
Завдання на самостійне рішення
Приклад 1. Дана окружність. Її центр – точка О. АС і BD – діаметри.
Приклад 2. Дані чотирикутник ABCD і коло, описане навколо нього.
Приклад 3. Дана окружність і вписаний чотирикутник ABCD. Два його кути рівні 82º і 58º. Необхідно знайти більший з решти кутів і записати відповідь у градусах.
Приклад 4. Даний чотирикутник ABCD. Кути А, В, С дано у співвідношенні 1:2:3. Необхідно знайти кут D, якщо зазначений чотирикутник може бути вписаний в окружність. Відповідь має бути дана в градусах.
Приклад 5. Даний чотирикутник ABCD. Його сторони утворюють дуги описаного кола. Градусні величини AB, BC, CD і AD, відповідно, дорівнюють: 78, 107, 39, 136. Слід знайти <З даного чотирикутника і записати відповідь у градусах.
