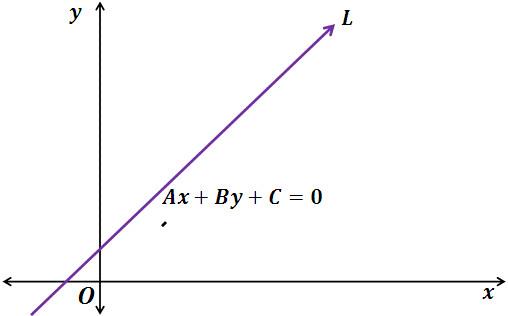Важливим геометричним об’єктом, який вивчають у плоскому просторі, є пряма. У тривимірному ж просторі, крім прямої, з’являється ще площину. Обидва об’єкти зручно задавати за допомогою направляючих векторів. Що це таке, як застосовують ці вектора для визначення рівнянь прямої і площини? Ці та інші питання висвітлюються у статті.
Пряма і способи її задавання
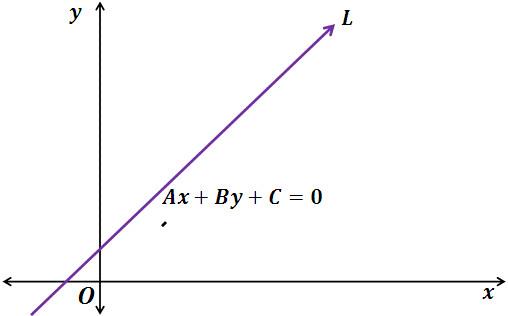
Кожен школяр добре представляє, про якому геометричному об’єкті йде мова. З точки зору математики, пряма являє собою набір точок, які в разі їх попарного довільного з’єднання між собою приводять до отримання сукупності паралельних векторів. Це визначення прямої використовують для написання рівняння для неї як у двовимірному, так і в тривимірному просторі.
Для опису даного одномірного об’єкта користуються різними видами рівнянь, які перераховані в списку нижче:
- загального виду;
- параметричне;
- векторне;
- канонічне або симетричне;
- у відрізках.
Кожен з названих видів має певні переваги по відношенню до інших. Наприклад, рівнянням у відрізках зручно користуватися при вивченні поведінки прямої відносно осей координат, рівняння загального виду зручно при знаходженні напрямку, перпендикулярного заданої прямої, а також при обчисленні кута її перетину з віссю x (для плоского випадку).
Оскільки тема цієї статті пов’язана з напрямним вектором прямої, то далі будемо розглядати тільки рівняння, де цей вектор є принциповим і міститься явно, тобто векторне вираз.
Завдання прямій через вектор
Припустимо, що у нас є деякий вектор v з відомими координатами (a; b; c). Оскільки координат три, то заданий вектор в просторі. Як зобразити його в прямокутній системі координат? Робиться це дуже просто: на кожній з трьох осей відкладається відрізок, довжина якого дорівнює відповідної координати вектора. Точка перетину трьох перпендикулярів, відновлених до площинах xy, yz і xz, буде кінцем вектора. Початком його є точка (0; 0; 0).
Тим не менш наведене положення вектора не є єдиним. Аналогічним чином можна намалювати v, розташовуючи його початок в довільній точці простору. Ці міркування говорять про те, що поставити конкретну пряму з допомогою вектора не можна. Він задає сімейство з нескінченного числа паралельних прямих.
Тепер зафіксуємо деяку точку P(x0; y0; z0) простору. І поставимо умову: через P повинна проходити пряма. У цьому випадку вектор v теж повинен містити цю точку. Останній факт означає, що можна поставити одну єдину пряму, використовуючи P і v. Вона запишеться у вигляді наступного рівняння:
Q = P + λ × v
Тут Q – будь-яка точка, що належить прямій. Цю точку можна отримати, підібравши відповідний параметр λ. Записане рівняння називається векторним, а v отримав назву направляючого вектора прямої. Розташовуючи так, щоб він проходив через P, і змінюючи його довжину за допомогою параметра λ, ми отримуємо кожну точку Q прямій.
В координатній формі рівняння запишеться так:
(x; y; z) = (x0; y0; z0) + λ × (a; b; c)
І в явному (параметричному вигляді можна записати:
x = x0 + λ × a;
y = y0 + λ × b;
z = z0 + λ × c
Якщо в наведених виразах виключити третю координату, то ми отримаємо векторні рівняння прямої на площині.
Для яких завдань корисно знати направляючий вектор ?
Як правило, це завдання на визначення паралельності та перпендикулярності прямих. Також визначає напрям прямої вектор використовується при обчисленні дистанції між прямими і точкою і прямою, для опису поведінки прямої відносно площини.
Дві прямі будуть паралельними, якщо такими є їх направляючі вектори. Відповідно, перпендикулярність прямих доводиться з допомогою перпендикулярності їх векторів. У цих типах завдань достатньо розрахувати скалярний добуток даних векторів, щоб отримати відповідь.
У разі задач на обчислення відстаней між прямими і точками направляючий вектор входить явно у відповідну формулу. Запишемо її:
d = |[P1P2 × v] | / |v|
Тут P1P2 – побудований на точках P1 і P2 спрямований відрізок. Точка P2 є довільною, що лежить на прямій з вектором v, точка ж P1 є тією, до якої слід визначити відстань. Вона може бути як самостійним, так і належати до іншої прямої або площини.
Зазначимо, що розраховувати відстань між прямими має сенс тільки тоді, коли вони є паралельними або мимобіжними. Якщо ж вони перетинаються, то d дорівнює нулю.
Наведена формула для d справедлива і для розрахунку дистанції між площиною і паралельної їй прямої, тільки в цьому випадку P1 повинна належати площині.
Вирішимо кілька завдань, щоб наочніше показати, як користуватися даним вектором.
Завдання на складання векторного рівняння
Відомо, що пряма описується наступним рівнянням:
y = 3 × x – 4
Слід написати відповідну вираз у векторній формі.
Це типове рівняння прямої, відоме кожному школяреві записано в загальному вигляді. Покажемо, як його переписати у векторній формі.
Вираз можна представити у вигляді:
(x; y) = (x; 3 × x – 4)
Видно, що якщо його розкрити, то вийде початкове рівність. Тепер розділимо його праву частину на два вектора так, щоб тільки один з них містив ікси, маємо:
(x; y) = (x; 3 × x) + (0; -4)
Залишається винести x за дужки, позначити його грецьким символом і поміняти вектора правій частині місцями:
(x; y) = (0; -4) + λ × (1; 3)
Ми отримали векторну форму запису вихідного виразу. Координати направляючого вектора прямої рівні (1; 3).
Завдання на визначення взаємного розташування прямих
У просторі задано дві прямі:
(x; y; z) = (1; 0; -2) + λ × (-1; 3; 1);
(x; y; z) = (3; 2; 2) + γ × (1; 2; 0)
Вони є паралельними, мимобіжними або перетинаються?
Ненульові вектори (-1; 3; 1) і (1; 2; 0) будуть напрямними для цих прямих. Виразимо в параметричній формі ці рівняння і підставимо координати першого в друге. Отримуємо:
x = 1 – λ;
y = 3 × λ;
z = -2 + λ;
————-
x = 3 + γ = 1 – λ => γ = -2 – λ;
y = 2 + 2 × γ = 3 × λ => γ = 3 / 2 × λ – 1;
z = 2 = -2 + λ => λ = 4
Підставляємо знайдений параметр λ два рівняння вище, отримуємо:
γ = -2 – λ = -6;
γ = 3 / 2 × λ – 1 = 5
Параметр γ не може одночасно приймати два різних значення. Це означає, що прямі не мають жодної спільної точки, тобто є мимобіжними. Паралельними вони не є, так як ненульові вектори не паралельні один одному (для їх паралельності повинно існувати число, яке б шляхом множення на один вектор призводило до координат другого).
Математичний опис площині
Для завдання площини у просторі наведемо рівняння загального виду:
A × x + B × y + C × z + D = 0
Тут великі латинські букви являють собою конкретні числа. Перші три з них визначають координати нормального вектора площини. Якщо позначити n, тоді:
n = (A; B; C)
Цей вектор є перпендикулярним площині, тому його називають напрямним. Його знання, а також відомі координати якої-небудь точки, що належить площині, однозначно задають останню.
Якщо точка P(x1; y1; z1) належить площині, тоді вільний член D розраховується наступним чином:
D = -1 × (A × x1 + B × y1 + C × z1)
Розв’яжемо декілька задач з використанням загального рівняння для площини.
Завдання на знаходження нормального вектора площини
Площина задана в наступному вигляді:
(y – 3) / 2 + (x + 1) / 3 – z / 4 = 1
Як знайти направляючий вектор для неї?
З наведеної вище теорії випливає, що координати нормального вектора n є коефіцієнтами, що стоять перед змінними. У зв’язку з цим для знаходження n слід записати рівняння в загальному вигляді. Маємо:
1 / 3 × x + 1 / 2 × y – 1 / 4 × z – 13 / 6 = 0
Тоді нормальний вектор площини дорівнює:
n = (1/3; 1/2; -1/4)
Завдання на складання рівняння площини
Дано координати трьох точок:
M1(1; 0; 0);
M2(2; -1; 5);
M3(0; -2; -2)
Як буде виглядати рівняння площині, що містить всі ці точки.
Через три точки, які не належать одній прямій, можна провести тільки одну площину. Щоб знайти її рівняння, спочатку обчислимо направляючий вектор площини n. Для цього зробимо наступним чином: знайдемо довільні два вектора, що належать площині, і обчислимо їх векторний добуток. Воно дасть вектор, який цій площині буде перпендикулярний, тобто n. Маємо:
M1M2 = (1; -1; 5); M1M3 = (-1; -2; -2);
n = [M1M2 × M1M3] = (12; -3; -3)
Візьмемо точку M1 для складання виразу площині. Отримуємо:
D = -1 × (12 × 1 + (-3) × 0 + (-3) × 0) = -12;
12 × x – 3 × y – 3 × z – 12 = 0 =>
4 × x – y – z – 4 = 0
Ми отримали вираз загального типу для площини у просторі, визначивши спочатку направляючий вектор для неї.
Властивість векторного добутку слід запам’ятати при вирішенні завдань з площинами, оскільки воно дозволяє простим способом визначати координати нормального вектора.
