Типовими лінійними параметрами будь піраміди є довжини сторін її заснування, висота, бічні ребра і апофемы. Тим не менше існує ще одна характеристика, яка пов’язана з зазначеними параметрами, – це двогранний кут. Розглянемо у статті, що він собою являє і як його знаходити.
Просторова фігура піраміда
Кожен школяр добре уявляє, про що йде мова, коли чує слово “піраміда”. Геометрично побудувати її можна так: вибрати деякий многокутник, потім зафіксувати точку в просторі і з’єднати її з кожним кутом багатокутника. Вийшла об’ємна фігура буде пірамідою довільного типу. Багатокутник, що її утворює, називається підставою, а точка, з якої з’єднані всі його кути, є вершиною фігури. Нижче на малюнку схематично показана п’ятикутна піраміда.
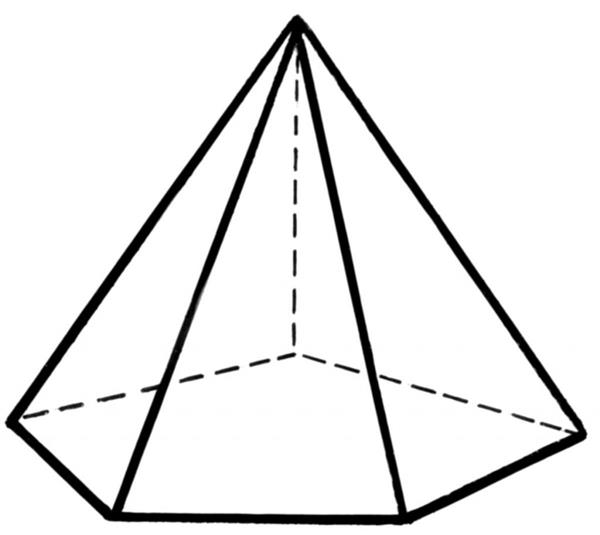
Видно, що її поверхня утворена не тільки пятиугольником, але і п’ятьма трикутниками. У загальному випадку число цих трикутників буде дорівнює кількості сторін багатокутного підстави.

