Коли в загальноосвітніх школах вивчають властивості упорядкованих послідовностей чисел, то в обов’язковому порядку розглядають так звану убуваючу нескінченну геометричну прогресію. Розкриємо детальніше це питання в статті.
Що таке геометрична прогресія?
Перед тим як переходити до пояснення нескінченної спадної геометричної прогресії, слід дати визначення цієї числової послідовності. Геометрична прогресія – це такий ряд чисел, у якому кожний наступний член однозначно виходить з попереднього шляхом множення його на деяке раціональне число. Це число називається знаменником.
Прикладом цього виду прогресії є наступний ряд чисел: 1, 4, 16, 64, … Видно, що якщо помножити будь-яке з цих чисел на 4, то виходить наступний член ряду. Це означає, що знаменник цієї послідовності знаходиться за формулою: r = an/an-1, тут an і an-1 – n-й і (n-1)-й члени прогресії.
Виходячи з визначення цього виду прогресії, можна n-й її член знайти, використовуючи наступне вираз: an = a1*r(n-1), тобто достатньо знати знаменник і перший член числового ряду.
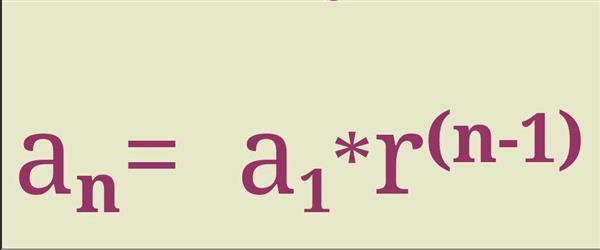
Наприклад, знайдемо 8-е число в геометричній прогресії, наведеною вище. Маємо: a8 = a1*r7 = 1*47 = 16384.
Ще однією важливою формулою для геометричній прогресії є вираз для знаходження суми її n перших членів. Ця формула має вигляд: Sn = a1*(rn-1)/(r-1). Застосуємо її для знаходження суми 8-ми чисел послідовності вище. Отримуємо: S8 = 1*(48-1)/(4-1) = 21845.