Одними з відомих ефектів, які підтверджують хвильову природу світла, є дифракція і інтерференція. Головна область їх застосування – спектроскопія, в якій для аналізу спектрального складу електромагнітного випромінювання використовують дифракційні решітки. Формула, яка описує положення головних максимумів, що даються цієї ґратами, розглядається в даній статті.
У чому полягають явища дифракції та інтерференції?
Перш ніж розглядати виведення формули дифракційної решітки, слід познайомитися з явищами, завдяки яким це решітка виявляється корисною, тобто з дифракцією і інтерференцією.
Дифракція – це процес зміни руху хвильового фронту, коли на своєму шляху він зустрічає непрозоре перешкоду, розміри якого порівнянні з довжиною хвилі. Наприклад, якщо через маленький отвір пропустити сонячне світло, то на стіні можна спостерігати не маленьку світну точку (що повинно було статися, якби світло поширювалося по прямій лінії), а світне пляма деяких розмірів. Цей факт свідчить про хвильової природи світла.
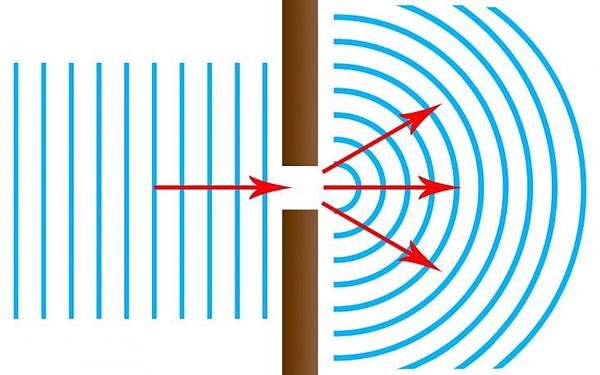
Інтерференція – ще одне явище, яке характерне виключно для хвиль. Його суть полягає в накладення хвиль один на одного. Якщо хвильові коливання від кількох джерел узгоджені (є когерентними), тоді можна спостерігати стійку картину з чергуються світлих і темних областей на екрані. Мінімуми на такій картині пояснюються приходом хвиль в дану точку в протифазі (pi і -pi), а максимуми є результатом попадання в розглянуту точку хвиль в одній фазі (pi та pi).
Обидва описаних явища вперше пояснив англієць Томас Юнг, коли дослідив дифракцію монохроматичного світла на двох тонких щілинах в 1801 році.
Принцип Гюйгенса-Френеля і наближення далекого і близького полів
Математичний опис явищ дифракції та інтерференції є нетривіальним завданням. Знаходження точного її рішення вимагає виконання складних розрахунків із залученням максвеллівської теорії електромагнітних хвиль. Тим не менш в 20-е роки XIX століття француз Огюстен Френель показав, що, використовуючи подання Гюйгенса про вторинних джерелах хвиль, можна з успіхом описувати ці явища. Ця ідея привела до формулювання принципу Гюйгенса-Френеля, який в даний час лежить в основі виведення всіх формул для дифракції на перешкодах довільної форми.
Тим не менш, навіть з допомогою принципу Гюйгенса-Френеля вирішити задачу дифракції в загальному вигляді не вдається, тому при одержанні формул вдаються до деяким наближенням. Головним з них є плоский хвильовий фронт. Саме така форма хвилі повинна падати на перешкоду, щоб можна було спростити ряд математичних викладок.
Наступне наближення полягає у положенні екрана, куди проектується дифракційна картина, щодо перешкоди. Це положення описується числом Френеля. Воно обчислюється так:
F = a2/(D*λ).
Де a – геометричні розміри перешкоди (наприклад, щілини або круглого отвору), λ – довжина хвилі, D – відстань між екраном і перешкодою. Якщо для конкретного експерименту F<<1 (1, тоді має місце наближення ближнього поля або дифракція Френеля.
Різниця між дифракциями Фраунгофера і Френеля полягає в різних умовах для явища інтерференції на маленькому і великій відстані від перешкоди.
Висновок формули головних максимумів дифракційної гратки, який буде наведено далі в статті, передбачає розгляд дифракції Фраунгофера.
Дифракційна решітка та її види
Ця сітка являє собою платівку зі скла або прозорого пластика розміром в декілька сантиметрів, на яку нанесені непрозорі штрихи однакової товщини. Штрихи розташовані на постійному відстані d один від одного. Це відстань носить назву періоду решітки. Два інших важливих характеристики приладу – це постійна гратки a і кількість прозорих щілин N. Величина a визначає кількість щілин на 1 мм довжини, тому вона обернено пропорційна періоду d.
Існує два типи дифракційних решіток:
- Прозора, яка описана вище. Дифракційна картина від такої решітки виникає в результаті проходження через неї хвильового фронту.
- Відображає. Вона виготовляється за допомогою нанесення маленьких борозенок на гладку поверхню. Дифракція і інтерференція від такої пластинки виникають за рахунок відбиття світла від вершин кожної борозенки.
Який би не був тип решітки, ідея її впливу на хвильовий фронт полягає у створенні періодичного збурення в ньому. Це призводить до утворення великої кількості когерентних джерел, результатом інтерференції яких є дифракційна картина на екрані.
Основна формула дифракційної решітки
Виведення цієї формули передбачає розгляд залежності інтенсивності випромінювання від кута його падіння на екран. У наближенні дальнього поля виходить наступна формула для інтенсивності I(θ):
I(θ) = I0*(sin(β)/β)2*[sin(N*α)/sin(α)]2, де
α = pi*d/λ*(sin(θ) – sin(θ0));
β = pi*a/λ*(sin(θ) – sin(θ0)).
У формулі ширина щілини дифракційної решітки позначається символом a. Тому множник в круглих дужках відповідає за дифракцію на одній щілині. Величина d – це період дифракційної решітки. Формула показує, що множник у квадратних дужках, де з’являється цей період, описує інтерференцію від сукупності щілин решітки.
Користуючись наведеною формулою, можна розрахувати значення інтенсивності для будь-якого кута падіння світла.
Якщо знаходити значення максимумів інтенсивності I(θ), то можна прийти до висновку, що вони з’являються за умови, що α = m*pi, де m є будь-яким цілим числом. Умови максимумів отримуємо:
m*pi = pi*d/λ*(sin(θm) – sin(θ0)) =>
sin(θm) – sin(θ0) = m*λ/d.
Отриманий вираз називається формулою максимумів дифракційної решітки. Числа m – це порядок дифракції.
Інші способи запису основної формули для решітки
Зауважимо, що наведена в попередньому пункті формулі присутній член sin(θ0). Тут кут θ0 відображає напрямок падіння фронту світлової хвилі відносно площини решітки. Коли фронт падає паралельно цій площині, то θ0 = 0o. Тоді отримуємо вираз для максимумів:
sin(θm) = m*λ/d.
Оскільки постійна гратки a (не плутати з шириною щілини) обернено пропорційна величині d, то через постійну дифракційної решітки вище формула перепишеться у вигляді:
sin(θm) = m*λ*a.
Щоб не виникало помилок при підстановці конкретних чисел λ, a і d у ці формули, слід завжди використовувати відповідні одиниці СІ.
Поняття про кутової дисперсії решітки
Будемо позначати цю величину буквою D. Згідно математичного визначенням, вона записується наступним рівністю:
D = dθm/dλ.
Фізичний сенс кутової дисперсії D полягає в тому, що вона показує, на який кут dθm зміститься максимум для порядку дифракції m, якщо змінити довжину падаючої хвилі на dλ.
Якщо застосувати цей вираз для рівняння решітки, тоді вийде формула:
D = m/(d*cos(θm)).
Кутова дисперсія дифракційної решітки визначається за формулою вище. Видно, що величина D залежить від порядку m і від періоду d.
Чим більша дисперсія D, тим вище роздільна здатність даної решітки.
Ґратка
Під роздільною здатністю розуміють фізичну величину, яка показує, на яку мінімальну величину можуть відрізнятися дві довжини хвилі, щоб їх максимуми на дифракційній картині з’являлися роздільно.
Роздільна здатність визначається критерієм Релея. Він говорить: два максимуму можна розділити на дифракційній картині, якщо відстань між ними виявляється більше напівширини кожного з них. Кутова напівширина максимуму для решітки визначається за формулою:
Δθ1/2 = λ/(N*d*cos(θm)).
Ґратка згідно з критерієм Релея дорівнює:
Δθm>Δθ1/2 або D*Δλ>Δθ1/2.
Підставляючи значення D і Δθ1/2, отримуємо:
Δλ*m/(d*cos(θm))>λ/(N*d*cos(θm) =>
Δλ > λ/(m*N).
Це і є формула роздільну здатність дифракційної решітки. Чим більше число штрихів N на платівці і чим вище порядок дифракції, тим більше роздільна здатність для даної довжини хвилі λ.
Дифракційна решітка в спектроскопії
Випишемо ще раз основне рівняння максимумів для решітки:
sin(θm) = m*λ/d.
Тут видно, що чим більше довжина хвилі падає на пластинку зі штрихами, тим при великих значеннях кутів будуть з’являтися максимуми на екрані. Іншими словами, якщо через пластинку пропустити немонохроматический світло (наприклад, білий), то на екрані можна бачити поява кольорових максимумів. Починаючи від центрального білого максимуму (дифракція нульового порядку), далі будуть з’являтися максимуми для більш коротких хвиль (фіолетовий, синій), а потім для більш довгих (оранжевий, червоний).
Інший важливий висновок із цієї формули полягає в залежності кута θm від порядку дифракції. Чим більше m, тим більше значення θm. Це означає, що кольорові лінії будуть сильніше розділені між собою на максимумах для високого порядку дифракції. Цей факт вже був освячений, коли розглядалася ґратка (див. попередній пункт).
Описані здатність дифракційної решітки дозволяють використовувати її для аналізу спектрів випромінювання різних об’єктів, що світяться, включаючи далекі зірки і галактики.
Приклад розв’язання задачі
Покажемо, як користуватися формулою дифракційної решітки. Довжина хвилі світла, яка падає ґрати, дорівнює 550 нм. Необхідно визначити кут, при якому з’являється дифракція першого порядку, якщо період d дорівнює 4 мкм.
Кут θ1 легко розрахувати за формулою:
θ1 = arcsin(λ/d).
Переводимо всі дані в одиниці СІ та підставляємо в це рівність:
θ1 = arcsin(550*10-9/(4*10-6)) = 7,9 o.
Якщо екран буде знаходитися на відстані 1 метр від решітки, то від середини центрального максимуму лінія першого порядку дифракції для хвилі 550 нм з’явиться на відстані 13,8 см, що відповідає куту 7,9 o.
