При розв’язанні задач на рух тіл в просторі часто використовують формули збереження кінетичної енергії і імпульсу. Виявляється, що аналогічні вирази існують і для обертових тел. У цій статті докладно розглядається закон збереження моменту імпульсу (формули відповідні також наводяться) і дається приклад розв’язання задачі.
Процес обертання і момент імпульсу
Перед тим як перейти до розгляду формули закону збереження моменту імпульсу, необхідно познайомитися з цим фізичним поняттям. Найпростіше його можна ввести, якщо скористатися малюнком нижче.
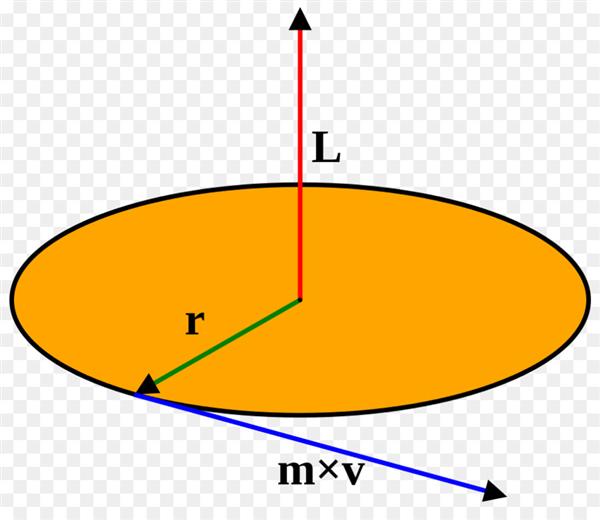
На малюнку видно, що на кінець вектора r, спрямованого від осі обертання і перпендикулярного їй, є деяка матеріальна точка масою m. Ця точка рухається по колу названого радіуса з лінійною швидкістю v. З фізики відомо, що добуток маси на лінійну швидкість називається імпульсом (p). Тепер варто ввести нову величину:
L = r*m*v = r*p.
Тут векторна величина L являє собою момент імпульсу. Щоб перейти до скалярної формі запису, що необхідно знати модулі відповідних значень r і p, а також кут θ між ними. Скалярна формула для L має вигляд:
L = r*m*v*sin(θ) = r*p*sin(θ).
На малюнку вище кут θ є прямим, тому можна просто записати:
L = r*m*v = r*p.
Із записаних виразів випливає, що одиницею вимірювання L будуть кг*м2/с.

