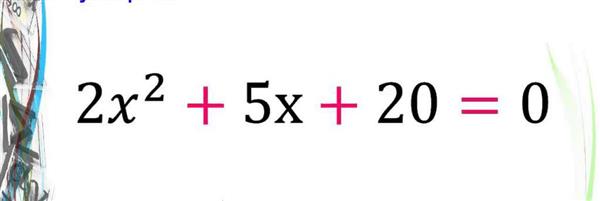Квадратні рівняння часто з’являються в ряді задач з математики і фізики, тому вміти їх вирішувати має кожен школяр. У цій статті докладно розглядаються основні методи розв’язування квадратних рівнянь, а також наводяться приклади їх використання.
Яке рівняння називається квадратним
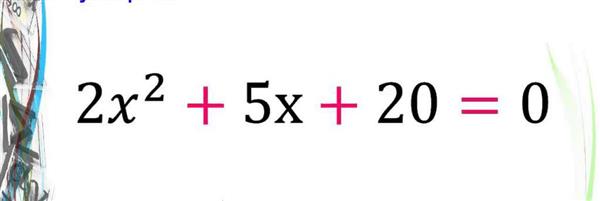
В першу чергу відповімо на питання цього пункту, щоб краще розуміти, про що піде мова в статті. Отже, квадратне рівняння має наступний загальний вигляд: c + b*x+a*x2=0, де a, b, c – деякі числа, які називаються коефіцієнтами. Тут a≠0 – це обов’язкова умова, в іншому випадку зазначене вироджується в рівняння лінійне. Інші коефіцієнти (b, c) можуть приймати абсолютно будь-які значення, включаючи нуль. Так, вирази типу a*x2=0, де b=0 і c=0 або c+a*x2=0,де b=0, або b*x+a*x2=0, де c=0 – це теж квадратні рівняння, які називають неповними, оскільки у них або лінійний коефіцієнт b дорівнює нулю, або нульовим є вільний член c, або вони обидва зануляются.
Рівняння, в якому a=1, називають наведеним, тобто воно має вигляд: x2 + з/a + (b/a)*x =0.
Рішення квадратного рівняння полягає в знаходженні таких значень x, які задовольняють його рівності. Ці значення називаються коренями. Оскільки розглянуте рівняння – це вираз другого ступеня, то це означає, що максимальне число його коріння не може перевищувати двох.