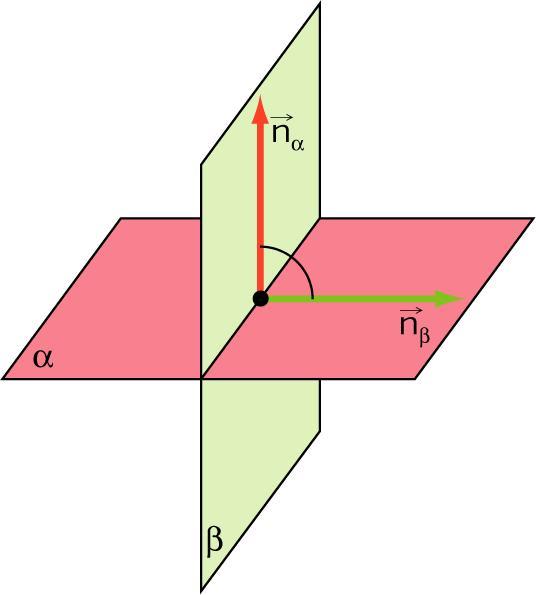
При рішенні геометричних задач в просторі часто зустрічаються такі, де необхідно розрахувати кути між різними просторовими об’єктами. У цій статті розглянемо питання знаходження кутів між площинами та між ними і прямий.
Пряма в просторі
Відомо, що абсолютно будь-яка пряма на площині може бути визначена наступним рівністю:
y = a * x + b
Тут a і b – деякі числа. Якщо уявити тим же самим виразом пряму в просторі, то вийде вже площина, паралельна осі z. Для математичного визначення просторової прямий застосовують інший спосіб рішення, ніж в двовимірному випадку. Він полягає у використанні поняття “направляючий вектор”.
Направляючий вектор прямої показує її орієнтацію в просторі. Цей параметр належить прямій. Оскільки існує безліч паралельних в просторі векторів, то для однозначного визначення даного геометричного об’єкта необхідно також знати координати точки, що належить йому.
Припустимо, що є точка P(x0; y0; z0) і направляючий вектор v(a; b; c), тоді рівняння прямої може бути задано наступним чином:
(x; y; z ) = P + α * v або
(x; y; z) = (x0; y0; z0) + α * (a; b; c)
Цей вираз називається параметричним векторним рівнянням прямої. Коефіцієнт α є параметром, який може приймати абсолютно будь-які дійсні значення. Координати прямої можна уявити явно, розкриваючи це рівність:
x = x0 + α * a;
y = y0 + α * b;
z = z0 + α * c