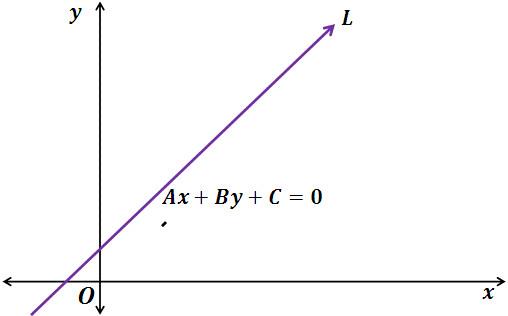Вміння знаходити відстань між різними геометричними об’єктами важливо, коли виконуються розрахунки площі поверхні фігур та їх обсягів. У цій статті розглянемо питання про те, як знаходити від точки до прямої відстань у просторі і на площині.
Математичний опис прямий
Щоб зрозуміти, як знаходити відстань від точки до прямої, слід розібратися з питанням математичного завдання цих геометричних об’єктів.
З точкою все просто, вона описується набором координат, число яких відповідає мірності простору. Наприклад, на площині це дві координати в тривимірному просторі – три.
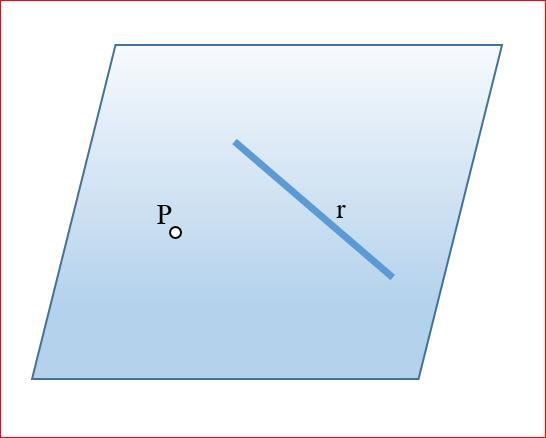
Що стосується одномірного об’єкта – прямий, то для її опису застосовують кілька видів рівнянь. Розглянемо лише два з них.
Перший вид називається векторним рівнянням. Нижче наведено вирази для прямих у тривимірному і двовимірному просторі:
(x; y; z) = (x0; y0; z0) + α × (a; b; c);
(x; y) = (x0; y0 ) + α × (a; b)
В цих виразах координати з нульовими індексами описують точку, через яку проходить задана пряма, набір координат (a; b; c) і (a; b) – це так звані вектора направляючі для відповідної прямої, α – це параметр, який може приймати будь-яке дійсне значення.
Векторне рівняння зручно в тому плані, що воно явно містить вектор напрямку прямої, координати якого можна використовувати при вирішенні завдань паралельності або перпендикулярності різних геометричних об’єктів, наприклад двох прямих.
Другий вид рівняння, який ми розглянемо для прямої, називається загальним. У просторі цей вид визначається загальними рівняннями двох площин. На площині ж він має наступну форму:
A × x + B × y + C = 0
Коли виконують побудову графіка, то його часто записують залежністю від ікси/игрека, тобто:
y = -A / B × x +(-C / B)
Тут вільний член -C / B відповідає координаті перетину прямої з віссю y, а коефіцієнт A / B пов’язаний з кутом нахилу прямої до осі x.