У шкільному курсі стереометрії однією з найпростіших фігур, яка має не нульові розміри уздовж трьох просторових осей, є чотирикутна призма. Розглянемо у статті, що це за фігура, з яких елементів вона складається, а також як можна розрахувати площу її поверхні та об’єм.
Поняття про призмі
В геометрії призмою вважають просторову фігуру, яка утворена двома однаковими підставами і бічними поверхнями, які з’єднують сторони цих підстав. Відзначимо, що обидва підстави переходять один в одного за допомогою операції паралельного перенесення на деякий вектор. Таке завдання призми призводить до того, що всі її бічні сторони завжди є параллелограммами.
Кількість сторін підстави може бути довільним, починаючи від трьох. При прагненні цього числа до безконечності, призма плавно переходить в циліндр, оскільки її основа стає колом, а бічні паралелограми, з’єднуючись, утворюють циліндричну поверхню.
Як і будь полиэдр, призма характеризується сторонами (площини, які обмежують фігуру), ребрами (відрізки, по яких перетинаються дві будь-які сторони) і вершинами (точки зустрічі трьох сторін, для призми дві з них є боковими, а третя – підставою). Кількості названих трьох елементів фігури зв’язані між собою наступним виразом:
Р = З + В – 2
Тут Р, С і В – це число ребер, сторін і вершин, відповідно. Цей вираз є математичним записом теореми Ейлера.
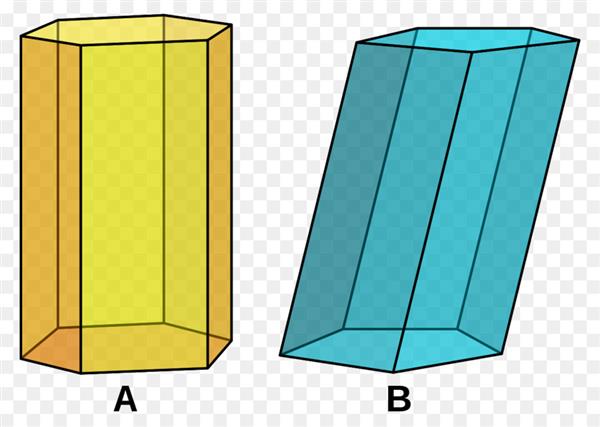
Вище наведений малюнок, де показано дві призми. В основі однієї з них (A) лежить правильний шестикутник, і сторони бічні перпендикулярні підстав. Малюнок B демонструє іншу призму. Її бічні сторони вже не перпендикулярні підстав, а підстава являє собою правильний п’ятикутник.

