Типовими геометричними завданнями на площині та у тривимірному просторі є проблеми визначення площ поверхонь різних фігур. У цій статті наведемо формулу площі бічної поверхні правильної чотирикутної піраміди.
Що собою являє піраміда?
Наведемо суворе геометричне визначення піраміди. Припустимо, що є деякий многокутник з n сторонами і з n кутами. Виберемо довільну точку простору, яка не буде знаходитися в площині зазначеного n-кутника, і з’єднаємо її з кожною вершиною багатокутника. Ми отримаємо фігуру, що має певний обсяг, яка називається n-вугільної пірамідою. Для прикладу покажемо на малюнку нижче, як виглядає п’ятикутна піраміда.
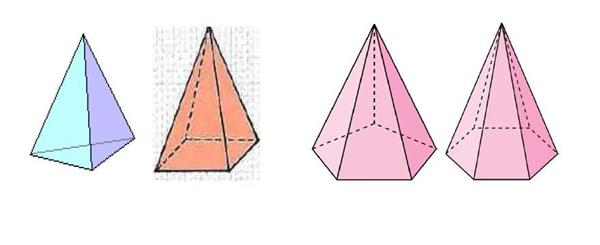
Два важливих елементи будь піраміди – це її основа (n-кутник) і вершина. Ці елементи з’єднані один з одним n трикутниками, які в загальному випадку не рівні один одному. Перпендикуляр, опущений з вершини до основи, називається висотою фігури. Якщо він перетинає основу в геометричному центрі (збігається з центром мас багатокутника), то таку піраміду називають прямою. Якщо, крім цього умови підстава є правильним гратки, то і вся піраміда називається правильною. Малюнок нижче показує, як виглядають правильні піраміди з трикутним, чотирикутним, п’ятикутним і шестикутним підставами.
Поверхню піраміди
Перш ніж переходити до питання про площу бічної поверхні правильної чотирикутної піраміди, слід докладніше зупинитися на понятті самої поверхні.
Як було сказано вище і показано на малюнках, будь-яка піраміда утворена набором граней або сторін. Одна сторона є підставою, і n сторін являють собою трикутники. Поверхню всієї фігури – це сума площ кожної її сторони.
Поверхня зручно вивчати на прикладі розгортки фігури. Розгортка для правильної чотирикутної піраміди наведена на зображення нижче.
Бачимо, що площа її поверхні дорівнює сумі чотирьох однакових площ рівнобедрених трикутників і площі квадрата.
Загальну площу всіх трикутників, які утворюють бокові сторони фігури, прийнято називати площею бічної поверхні. Далі покажемо, як її розрахувати для правильної чотирикутної піраміди.
Площа бічної поверхні правильної чотирикутної піраміди
Щоб обчислити площу бічної поверхні зазначеної фігури, знову звернемося до наведеної вище розгортці. Припустимо, що нам відома сторона квадратного підстави. Позначимо її символом a. Видно, що кожен з чотирьох однакових трикутників, має основу довжиною a. Щоб обчислити їх загальну площу, необхідно знати цю величину для одного трикутника. З курсу геометрії відомо, що площа трикутника St дорівнює добутку основи на висоту, яке слід поділити навпіл. Тобто:
St = 1/2*hb*a.
Де hb – висота рівнобедреного трикутника, проведена до основи a. Для піраміди ця висота є апотемой. Тепер залишається помножити отриманий вираз на 4, щоб отримати площа Sb поверхні бічної для даної піраміди:
Sb = 4*St = 2*hb*a.
Ця формула містить два параметри: апотему і сторону основи. Якщо остання в більшості умов завдань відома, то першу доводиться обчислювати, знаючи інші величини. Наведемо формули для розрахунку апотемы hb для двох випадків:
- коли відома довжина бічного ребра;
- коли відома висота піраміди.
Якщо позначити довжину бічного ребра (сторона рівнобедреного трикутника) символом L, тоді апотема hb визначитися за формулою:
hb = √(L2 – a2/4).
Це вираження є результатом застосування теореми Піфагора для трикутника бічній поверхні.
Якщо відома висота h піраміди, тоді апотему hb можна розрахувати так:
hb = √(h2 + a2/4).
Отримати цей вираз також не складно, якщо розглянути всередині піраміди прямокутний трикутник, утворений катетами h і a/2 і гіпотенузою hb.
Покажемо, як застосовувати ці формули, вирішивши дві цікаві завдання.
Завдання з відомою площею поверхні
Відомо, що площа бічної поверхні правильної чотирикутної піраміди дорівнює 108 см2. Необхідно обчислити значення довжини її апотемы hb, якщо висота піраміди дорівнює 7 див.
Запишемо формулу площі Sb поверхні бічної через висоту. Маємо:
Sb = 2*√(h2 + a2/4) *a.
Тут ми просто підставили відповідну формулу апотемы у вираз для Sb. Піднесемо обидві частини рівності до квадрату:
Sb2 = 4*a2*h2 + a4.
Щоб знайти значення a, зробимо заміну змінних:
a2 = t;
t2 + 4*h2*t – Sb2 = 0.
Тепер підставляємо відомі значення і вирішуємо квадратне рівняння:
t2 + 196*t – 11664 = 0.
t ≈ 47,8355.
Ми виписали тільки позитивний корінь рівняння. Тоді сторони основи піраміди дорівнює:
a = √t = √47,8355 ≈ 6,916 див.
Щоб отримати довжину апотемы, досить скористатися формулою:
hb = √(h2 + a2/4) = √(72 + 6,9162/4) ≈ 7,808 див.
Бічна поверхня піраміди Хеопса
Визначимо значення площі поверхні бічної для найбільшої єгипетської піраміди. Відомо, що в її основі лежить квадрат з довжиною сторони 230,363 метра. Висота споруди спочатку становила 146,5 метра. Підставимо ці цифри у відповідну формулу для Sb, отримаємо:
Sb = 2*√(h2 + a2/4) *a = 2*√(146,52+230,3632/4)*230,363 ≈ 85860 м2.
Знайдене значення трохи більше площі 17 футбольних полів.
